Stay hungry,stay foolish.

0%

并查集学习笔记--以NOI2001食物链为例

发表于 更新于 阅读次数： Valine：

先来简单定义一下并查集。

定义

并查集是一种树型的数据结构，用于处理一些不相交集合（Disjoint Sets）的合并及查询问题。

简而言之，就是用来判断两个元素是否处于同一个集合，就好像根据血缘判断两个人是否是亲戚一样。

主要操作

  • 查询元素A与元素B是否在同一集合中
  • 合并元素A与元素B所在的组

并查集的代码实现

一、初始化

准备一个数组储存每个节点的父节点，令他们等于其本身

1
2
3
for(int i = 0;i < n;i++){
    p[i]=i;
}

二、合并

并查集是树形结构，将两元素合并，就是从其中一个元素的根向另一个元素的根连边。如下图所示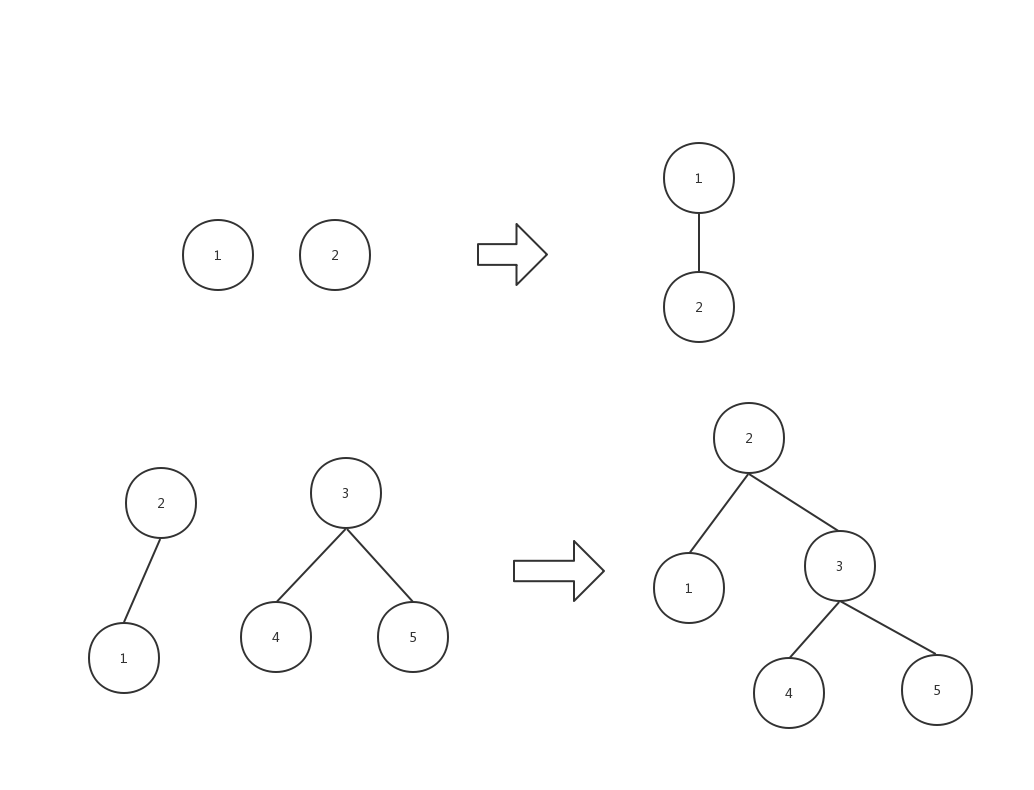

实现代码如下

1
2
3
4
5
6
7
8
void unite(int x,int y){
    x=find(x);
    y=find(y);
    if(x==y){
        return;
    }
    p[y]=x;
}

三、查询

为了查询两个节点是否属于同一组，我们需要找到树根。若两个节点属于同一个根，则说明他们在同一个集合里。通过递归调用我们可以找到它的根。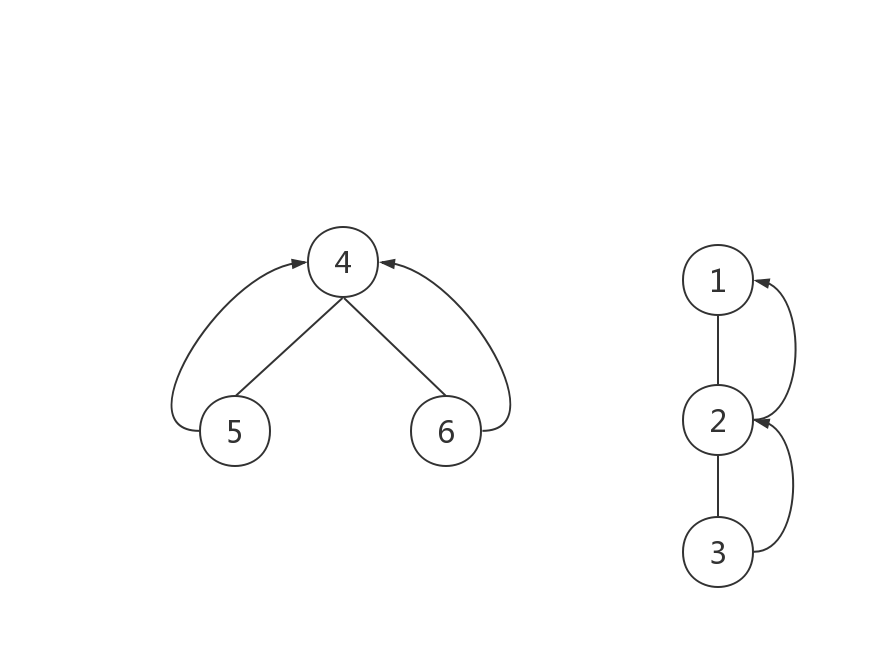

实现代码如下

1
2
3
4
5
6
int find(int x){
    if(x!=p[x]){
        return find(p[x]);
    }
    else return x;
}

四、优化

我们知道，当树退化成一条链时，查询操作将变得十分低效。如下图，同样的根节点，查找节点6的根节点的效率却天差地别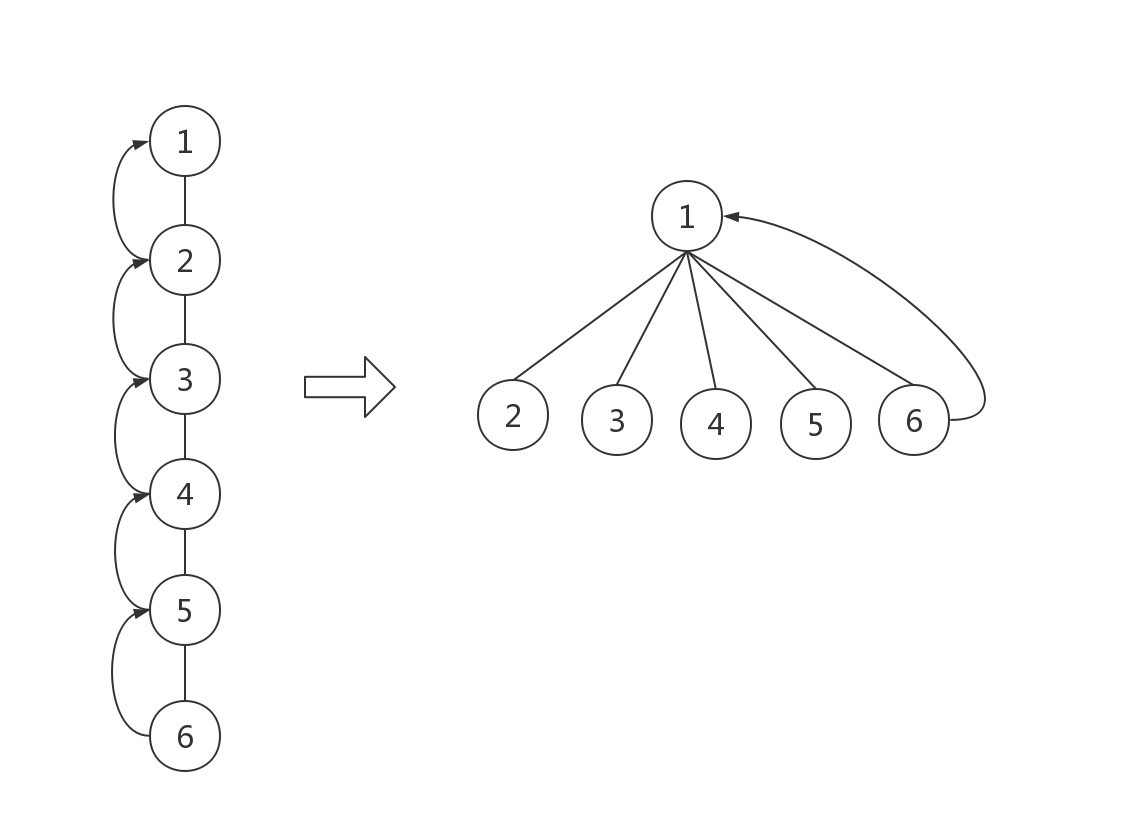

我们希望每个子节点都直接与根节点相连，这样就能达到效率最大化，也称之为路径压缩。这一步可以在查询的时候完成，我们既然查询到了它的根结点，我们可以直接修改它的父节点为根节点，只需对代码进行小小的改动：

1
2
3
4
5
6
int find(int x){
    if(x!=p[x]){
        return p[x]=find(p[x]);
    }
    else return x;
}

合并的操作也可以优化。我们可以新增一个数组Rank，合并时比较两棵树的高度Rank，将Rank小的向rank大的连边：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void unite(int x,int y){
    x=find(x);
    y=find(y);
    if(x==y){
        return;
    }
    if(rank[x]< rank[y]){
        p[x]=y;
    }
    else{
        p[y]=x;
        if(rank[x]==rank[y]){
            rank[x]++;
        }//如果两树高度相同，合并后易知其高度+1
    }
}

例题:食物链

题目描述

动物王国中有三类动物A,B,C，这三类动物的食物链构成了有趣的环形。A吃B， B吃C，C吃A。
现有N个动物，以1－N编号。每个动物都是A,B,C中的一种，但是我们并不知道它到底是哪一种。
有人用两种说法对这N个动物所构成的食物链关系进行描述：
第一种说法是”1 X Y”，表示X和Y是同类。
第二种说法是”2 X Y”，表示X吃Y。
此人对N个动物，用上述两种说法，一句接一句地说出K句话，这K句话有的是真的，有的是假的。当一句话满足下列三条之一时，这句话就是假话，否则就是真话。
1） 当前的话与前面的某些真的话冲突，就是假话；
2） 当前的话中X或Y比N大，就是假话；
3） 当前的话表示X吃X，就是假话。
你的任务是根据给定的N（1 <= N <= 50,000）和K句话（0 <= K <= 100,000），输出假话的总数。

输入格式

第一行是两个整数N和K，以一个空格分隔。
以下K行每行是三个正整数 D，X，Y，两数之间用一个空格隔开，其中D表示说法的种类。
若D=1，则表示X和Y是同类。
若D=2，则表示X吃Y。

输出格式

一行，一个整数，表示假话的总数。

输入样例

1
2
3
4
5
6
7
8
100 7
1 101 1 
2 1 2
2 2 3 
2 3 3 
1 1 3 
2 3 1 
1 5 5

输出样例

1
3

显然，我们无法完全确认动物到底在哪个类中，只能根据他们之间的关系推断结论是否正确，普通的并查集是远远不够的，这时候我们需要用到带权并查集。

带权并查集

概念

当节点之间的关系可以被量化且合并转移时，我们可以使用结点储存权值信息的并查集来维护节点之间的关系。

分析

我们用1表示A吃B，2表示A被B吃，0表示A与B是同类。
先考虑路径压缩时的转移方式,以从3连接到1时发生的转移

我们可以列出下表

2与根结点的关系 3与2的关系 3与根结点的关系
0 0 0
0 1 1
0 2 2
1 0 1
1 1 2
1 2 0
2 0 2
2 1 0
2 2 1

可以推出v[31]=(v[32]+v[21])%3

再来考虑下合并时发生的关系转移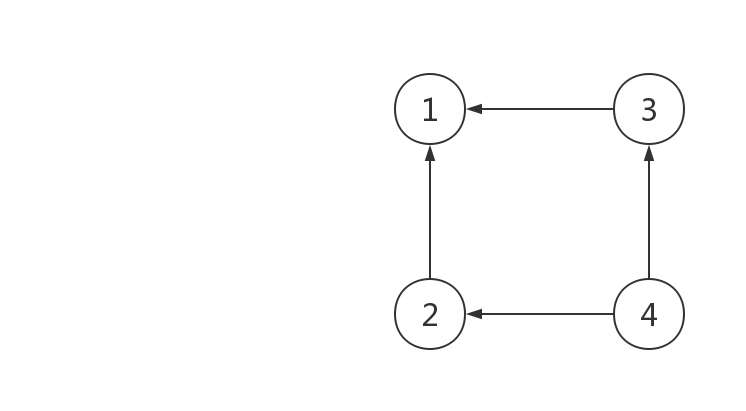

2与根结点的关系 4与2的关系 4与根结点的关系 2的根结点与4的根结点的关系
0 0 0 0
0 1 1 0
0 2 2 0
1 0 1 0
1 1 2 0
1 2 0 0
2 1 2 2
2 1 0 0
2 2 0 1

(不完全统计)
可以推出v[31]=(v[43]-v[21]-v[42])%3
为防止负数出现导致结果错误，这里应该加个6（易知不影响结果），即v[31]=(v[43]-v[21]-v[42]+6)%3。

那么我们要如何推断出同一集合中两个节点的关系呢?

2与根结点的关系 3与根结点的关系 2与3的关系
0 0 0
0 1 1
0 2 2
1 1 0
1 2 1
1 0 2
2 2 0
2 0 1
2 1 2

同理可推出v[23]=(v[31]-v[21])%3
防止负数，这里只用+3即可，即v[23]=(v[31]-v[21]+3)%3。

之后的事情就好办啦!对于每一组询问，若A，B不在同一个集合里，就合并他们；若A，B在一个集合里，就查询他们之间的关系，是否等于询问所给的关系，不对应便计数即可。询问中给的d减去1便是我们带权并查集中的权值。

AC代码

Code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
int find(int x,int p[],int v[]){
    if(x!=p[x]){
        int t = p[x];
        p[x] = find(p[x], p, v);
        v[x] = (v[x] + v[t]) % 3;
    }
    return p[x];
}
int main(){
    int n, k, ans = 0, i;
    cin >> n >> k;
    int p[n + 1], v[n + 1];
    memset(v, 0, sizeof(v));
    for (i = 1; i <= n;i++){
        p[i] = i;
    }
        while (k > 0)
        {
            int d, x, y;
            scanf("%d%d%d", &d, &x, &y);
            if (x > n || y > n||(x==y&&d==2))
            {
                ans++;
                k--;
                continue;
            }
            else{
                int fx = find(x,p,v);
                int fy = find(y,p,v);
                if(fx!=fy){
                    p[fy] = fx;
                    v[fy] = (6 + v[x] - v[y] - d + 1) % 3;
                }
                else if((v[x]-v[y]+3)%3!=d-1){
                    ans++;
                }
            }
            k--;
        }
    cout << ans;
    return 0;
}

</details>
个人比较懒~合并操作没有单独写个函数，合并优化也没写，嗯，还是过了。