Stay hungry,stay foolish.

0%

树状数组&线段树学习笔记

发表于 更新于 阅读次数： Valine：

先来看看我们需要解决的问题

P3374【模板】树状数组 1

如题，已知一个数列，你需要进行下面两种操作：

  • 将某一个数加上 $x$。
  • 求出某区间每一个数的和。

输入格式

第一行包含两个整数$n,m$分别表示该数列数字的个数和操作的总个数。

第二行包含$n$个用空格分隔的整数，其中第$i$个数字表示数列第$i$项的初始值。

接下来$m$行每行包含$3$个整数，表示一个操作，具体如下：

1 x k：将第$x$个数加上$k$。
2 x y：输出区间$[x, y]$内每个数的和。

输出格式
输出包含若干行整数，即为所有操作 2 的结果。

输入输出样例
输入 #1

1
2
3
4
5
6
7
5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4

输出 #1

1
2
14
16

数据很大，用遍历的话查询$O(n)$的复杂度下肯定是会超时的。考虑前缀和，修改的复杂度又变成了$O(n)$，无法解决问题。
那什么可以减小时间复杂度呢？那就是树形逻辑结构，树上的操作大多都是$O(logn)$级别的，而今天的主角之一——树状数组就出场啦。

首先我们来介绍lowbit(x)函数，它代表求二进制下x最低位的1及其后面的0所构成的新数字。
而根据计算机编码的性质，lowbit(x) = x&(-x)

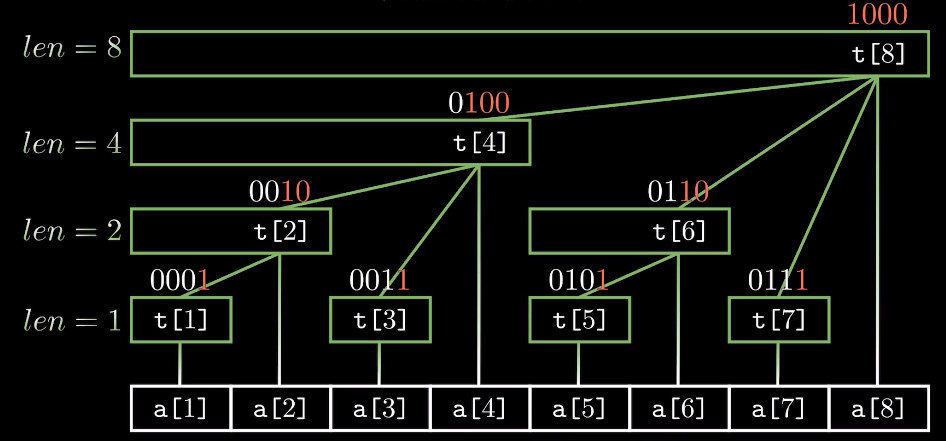
考虑这样的结构

图源来自网络，侵删

下方的a数组代表原数组，上方的t数组代表对应的树状数组,而其覆盖的区域代表了它所管理的前缀和区间。
观察可以发现，每个t数组的元素管理的区间长度为它二进制下最低位的1及后面的零构成的数字,即lowbit(x)。如
$3->0011->1->1$
$6->0110->10->2$

而每个节点的父节点编号就等于x+lowbit(x)。如
$6(0110)=5(0101)+1(1)$
$4(0100)=2(0010)+2(10)$

以及，每个区间的上一个与它不相交的最大区间编号为x-lowbit(x)。如
$6(0110)=7(0111)-1(1)$
$4(0100)=6(0110)-2(10)$

这样一来 我们就可以以$O(logn)$的复杂度进行查询和修改了
例如查询1~7的前缀和，不就是t[4]+t[6]+t[7]嘛？根据性质3很容易写出代码

1
2
3
4
5
6
long long sum(int x){
    long long ans = 0;
    for(; x; x -= x & -(x))
        ans += t[x];
    return ans;
}

而对于单点修改，除了修改本身之外，还需要将修改上传到它的父节点，由性质2即可得到代码

1
2
3
4
void add(int x, int v){
    for(; x <= n; x += x & -(x))
        t[x] += v;
}

初始化很简单，将数组里所有元素依次add上去即可。

AC代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include<iostream>
using namespace std;
int n, m;
long long t[500010];

void update(int x,int k){
    for (; x <= n;x += x & -x)
        t[x] += k;
}

long long query(int x){
    long long ans = 0;
    for (; x; x -= x & -x)
        ans += t[x];
    return ans;
}

int main(){
    cin.tie(0);
    ios::sync_with_stdio(false);
    int x, y, j;
    cin >> n >> m;
    for (int i = 1; i <= n;i++){
        cin >> x;
        update(i, x);
    }
    for (int i = 0; i < m;i++){
        cin >> j >> x >> y;
        if(j==1){
            update(x, y);
        }
        else{
            cout << query(y) - query(x-1) << "\n";
        }
    }
}

新的问题又来了,如果我们改为区间修改，单点查询的话，树状数组还适用吗？

P3368【模板】树状数组 2

如题，已知一个数列，你需要进行下面两种操作：

  • 将某区间每一个数数加上$x$；

  • 求出某一个数的值。

即使是树状数组，区间修改也需要$O(nlogn)$。有什么方法能更快的完成区间修改呢？那就是差分。
我们利用树状维护数组a的差分数组即可，当查询a[x]时，即是求x的前缀和。

AC代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include<iostream>
using namespace std;
long long t[500010];
int n,m,a[500010],ins,x,y,z;

void update(int x, int v){
    for(;x<=n;x+=x&-x)
        t[x]+=v;
}

long long query(int x){
    long long ans=0;
    for(;x;x-=x&-x)
        ans+=t[x];
    return ans;
}

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        cin>>a[i];
    }
    for(int i=0;i<m;i++){
        cin>>ins;
        if(ins==1){
            cin>>x>>y>>z;
            update(x,z);
            update(y+1,-z);
        }
        else{
            cin>>x;
            cout<<a[x]+query(x)<<"\n";
        }
    }
}

P3372【模板】线段树 1

如题，已知一个数列，你需要进行下面两种操作：

  • 将某区间每一个数数加上$k$；

  • 求出某区间每一个数的和。

输入格式

第一行包含两个整数$n,m$分别表示该数列数字的个数和操作的总个数。

第二行包含$n$个用空格分隔的整数，其中第$i$个数字表示数列第$i$项的初始值。

接下来$m$行每行包含$3$或$4$个整数，表示一个操作，具体如下：

1 x y k：将区间$[x, y]$内每个数加上$k$。
2 x y：输出区间$[x, y]$内每个数的和。

输出格式
输出包含若干行整数，即为所有操作 2 的结果。

输入输出样例
输入 #1

1
2
3
4
5
6
7
5 5
1 5 4 2 3
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4

输出 #1

1
2
3
11
8
20

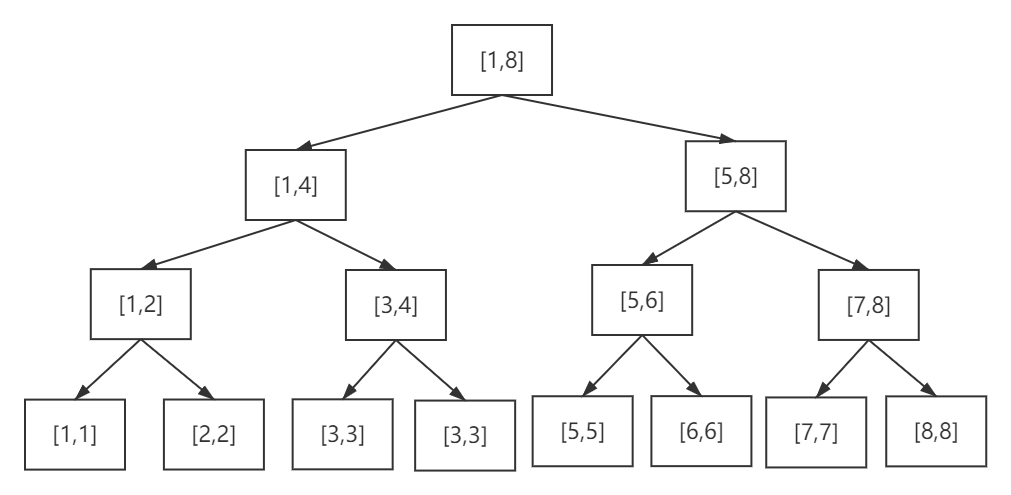
麻烦来了，又是区间修改又是区间查询，树状数组也难以同时完成这两个要求，这时候就要请我们今天的第二个主角——线段树出场了。
与树状数组不同的是，线段树是一种真实的树形结构，是一颗二叉树。

可以看到，线段树的每个节点都代表了一个区间。而每个节点的左右子节点代表了当前区间的左子区间和右子区间，而每个叶子节点储存的是数组元素。

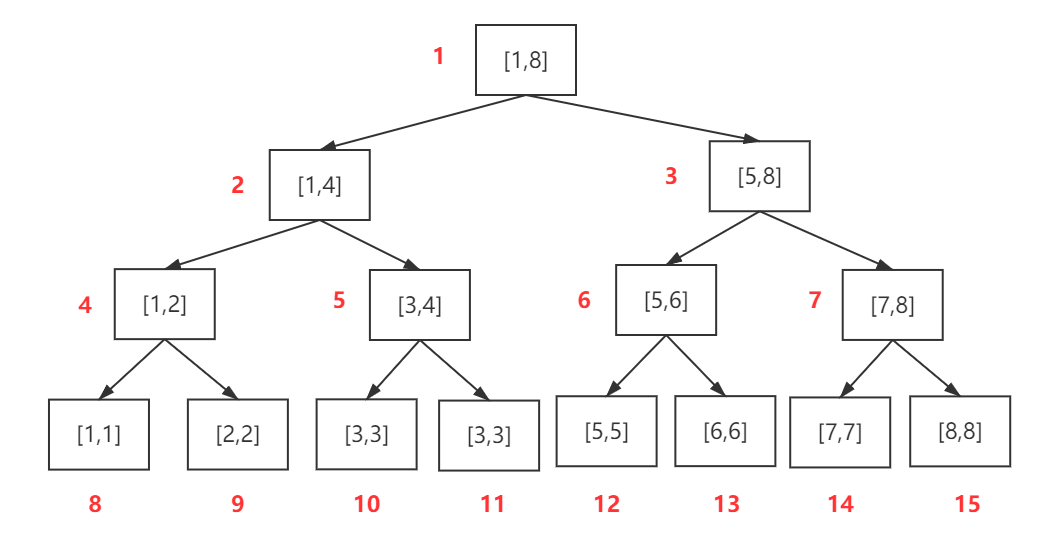
利用数组来储存线段树，从上到下，从左到右对节点进行编号，那么对于一个节点$p$，不难发现它的左右子节点编号分别为$2p$和$2p+1$。为了减少操作调用的参数，我们建立结构体记录每个节点的区间起点与终点，以它作为每一个基础节点。

1
2
3
4
struct segmentTree{
    int l, r;
    long long add, v;
};

那么我们来考虑如何建树，先给出代码

1
2
3
4
5
6
7
8
9
10
11
12
void build(int p,int l,int r){
    t[p].l = l; //初始化维护区间
    t[p].r = r;
    if(l==r){   //区间大小为1，赋初始值
        t[p].v = a[l];
        return;
    }
    int mid = l + r >> 1; //右移一位，除2并向下取整
    build(p * 2, l, mid);   //递归建立左子树
    build(p * 2 + 1, mid + 1, r);   //递归建立右子树
    t[p].v = t[p * 2].v + t[p * 2 + 1].v; //初始化区间和
}

从节点1开始递归建立，由父节点可以推知子节点的编号，以及其区间长度，递归赋值即可。若遇到区间长度为1的，说明为叶节点，直接赋予对应数组元素的值即可。左右子树建立完毕后，最后根据子节点的值计算父节点的值。

再考虑如何进行区间的修改。当节点的维护区间被指定的更新区间覆盖时，我们可以直接对整个区间进行更新。如区间的每一个数加上一个数$k$，即是区间和加上 $k区间长度=k(r-l+1)$。
那么当当前区间不被更新区间所覆盖的时候呢？将当前区间的中点与更新区间的起点与终点进行比较，决定是否要递归遍历当前区间的左右子区间即可，直到更新区间覆盖当前区间为止。
最后，不要忘记更新父节点的值。

等等，还有一个问题，我们是修改了当前区间的值，可是当查询该区间下的子区间的值，实际上是没有改变的。可是如果我们要将其下子区间的值全部修改，那么花费的时间复杂度也将增长到$O(nlogn)$，线段树就失去了它的意义。这时候我们引入一个”layztag”——懒标记来解决这个问题。

还记得前面结构体中定义的add吗？当我们准备对一个区间加$k$时，我们对它的add标记同样加上$k$。当查询或者修改涉及该节点的子区间时，我们就下传这个add，即在操作前对子区间加上add的值，并同样更新子节点的add，这样就能保证查询和修改操作的正确性。我们可以专门写一个pushdown(p)来完成这个工作，代码如下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
void pushdown(int p){
    if(t[p].add){
        t[p * 2].v += t[p].add * (t[p * 2].r - t[p * 2].l + 1);  //下传懒标记，实际值为区间长*区间要加上的值
        t[p * 2 + 1].v += t[p].add * (t[p * 2 + 1].r - t[p * 2 + 1].l + 1);
        t[p * 2].add += t[p].add;   //为子区间打上懒标记
        t[p * 2 + 1].add += t[p].add;
        t[p].add = 0; //懒标记下传完毕，清零
    }
}

void update(int p, int x, int y, int z){
    if(x<=t[p].l&&y>=t[p].r){   //如果当前区间被更新区间覆盖
        t[p].v += (long long)z * (t[p].r - t[p].l + 1);    //更新节点值，并且打上懒标记
        t[p].add += z;
        return;
    }
    pushdown(p);    //下传懒标记
    int mid = t[p].l + t[p].r >> 1; //表示左右子树代表的区间的中值
    if(x<=mid)  //如果x小于中值，说明修改涉及到左区间
        update(p * 2, x, y, z);
    if(y>mid)   //如果y小于中值，说明修改涉及到右区间
        update(p * 2 + 1, x, y, z);
    t[p].v = t[p * 2].v + t[p * 2 + 1].v; //更新完毕，最后更新父节点的值
}

最后，我们看看如何利用线段树进行区间查询。

1
2
3
4
5
6
7
8
9
10
11
12
long long query(int p,int x,int y){
    if(x<=t[p].l&&y>=t[p].r)    //当前区间被查询区间覆盖，返回区间和
        return t[p].v;
    pushdown(p);
    int mid = t[p].l + t[p].r >> 1;
    long long ans = 0;
    if(x<=mid)
        ans += query(p * 2, x, y);
    if(y>mid)
        ans += query(p * 2 + 1, x, y);
    return ans;
}

大体思路与修改操作一致，只不过当区间覆盖时返回的是区间的值而已。在查询前同样需要检测懒标记是否下传。

Extra Tip:对于一个长度为n的数组，应建立长度为4n的线段树数组。

AC代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
#include<iostream>
using namespace std;
struct segmentTree{
    int l, r;
    long long add, v;
};
int a[100010];
segmentTree t[400010];
void build(int p,int l,int r){
    t[p].l = l; //初始化维护区间
    t[p].r = r;
    if(l==r){   //区间大小为1，赋初始值
        t[p].v = a[l];
        return;
    }
    int mid = l + r >> 1; //右移一位，除2并向下取整
    build(p * 2, l, mid);   //递归建立左子树
    build(p * 2 + 1, mid + 1, r);   //递归建立右子树
    t[p].v = t[p * 2].v + t[p * 2 + 1].v; //初始化区间和
}

void pushdown(int p){
    if(t[p].add){
        t[p * 2].v += t[p].add * (t[p * 2].r - t[p * 2].l + 1);  //下传懒标记，实际值为区间长*区间要加上的值
        t[p * 2 + 1].v += t[p].add * (t[p * 2 + 1].r - t[p * 2 + 1].l + 1);
        t[p * 2].add += t[p].add;   //为子区间打上懒标记
        t[p * 2 + 1].add += t[p].add;
        t[p].add = 0; //懒标记下传完毕，清零
    }
}

void update(int p, int x, int y, int z){
    if(x<=t[p].l&&y>=t[p].r){   //如果当前区间被更新区间覆盖
        t[p].v += (long long)z * (t[p].r - t[p].l + 1);    //更新节点值，并且打上懒标记
        t[p].add += z;
        return;
    }
    pushdown(p);    //下传懒标记
    int mid = t[p].l + t[p].r >> 1; //表示左右子树代表的区间的中值
    if(x<=mid)  //如果x小于中值，说明修改涉及到左区间
        update(p * 2, x, y, z);
    if(y>mid)   //如果y小于中值，说明修改涉及到右区间
        update(p * 2 + 1, x, y, z);
    t[p].v = t[p * 2].v + t[p * 2 + 1].v; //更新完毕，最后更新父节点的值
}

long long query(int p,int x,int y){
    if(x<=t[p].l&&y>=t[p].r)    //当前区间被查询区间覆盖，返回区间和
        return t[p].v;
    pushdown(p);
    int mid = t[p].l + t[p].r >> 1;
    long long ans = 0;
    if(x<=mid)
        ans += query(p * 2, x, y);
    if(y>mid)
        ans += query(p * 2 + 1, x, y);
    return ans;
}

int main(){
    std::ios::sync_with_stdio(false);
    int n, m, z, x, y, k;
    cin >> n >> m;
    for (int i = 1; i <= n;i++){
        cin >> a[i];
    }
    build(1, 1, n);
    for (int i = 0; i < m;i++){
        cin >> z;
        if(z==1){
            cin >> x >> y >> k;
            update(1, x, y, k);
        }
        else{
            cin >> x >> y;
            cout << query(1, x, y) << "\n";
        }
    }
}